The various relationships between internal energy (U), enthalpy (H), Helmholtz free energy (a) and Gibbs free energy (g), with relevant parameters such as entropy, pressure, temperature and volume are given by the following equations:
1. dU = TdS – PdV
2. dH = TdS + VdP
3. dA = – SdT – PdV
4. dG = – SdT + VdP
If V is constant so that dV is zero, then eq. 1 will become:
(∂U / ∂S)V = T …………………………………………………………………………………………… (5)
If S is constant so that dS is zero, then eq.1 will become:
(∂U / ∂V)S = – P …………………………………………………………………………………………. (6)
Differentiating equation (5) with respect to V keeping S constant we will get:
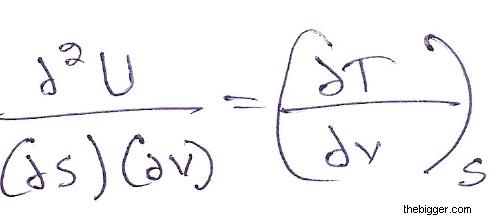
…………………………………………………………………….. (7)
Differentiating equation (6) with respect to S keeping V constant, we will get:
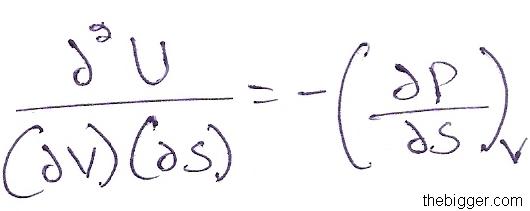
…………………………………………………………………. (8)
From the equation (7) and (8) we can conclude that:
(∂T / ∂V) S = – (∂P / ∂S) V …………………………………………………… (10)
Similarly we can obtain the following expressions:
(∂T / ∂P) S = (∂V / ∂S) P from equation (2) ……………………………………………… (11)
(∂S / ∂V) T = (∂P / ∂T) V from equation (3)……………………………………………… (12)
(∂S / ∂P) T = – (∂V / ∂T) P from equation (4) …………………………………………… (13)
Equations (10), (11), (12), (13) are known as Maxwell’s relationships.
Another set of Maxwell’s relationships, which can be derived from equations (1) to (4) are as follows:
(∂U / ∂S) V = (∂H / ∂S) P from equation (1) and (2) ………………………………… (14)
(∂U / ∂V) S = (∂A / ∂V) T from equation (1) and (3) ………………………………… (15)
(∂H / ∂P) S = (∂G / ∂P) T from equation (2) and (4) ………………………………… (16)
(∂A / ∂T) V = (∂G / ∂T) P from equation (3) and (4) ………………………………… (17)


