Cyclic process:
When a system returns to its original state after completing a series of changes, then it is known that a cycle is completed. This process is known as cyclic process. In a cyclic process the initial and the final state is same. As the internal energy U of the system depends only on the state of the system so in a cyclic process the net change of internal energy ∆U will be equal to zero i.e. ∆U = 0. Hence from the first law:
∆U = 0 = q + w
Hence, q = – w
If the process is taking place at constant temperature then the cycle is known as isothermal cycle. If the process is taking place reversibly then cycle is known as reversible cycle.
Example of the cyclic process:
The Carnot cycle is the best example of the cyclic process which is explained below:
The Carnot cycle:
The cycle was first discovered by a French engineer Sadi Carnot in 1824 which works on reversible cycle and is known as Carnot cycle.
Carnot employed a reversible cycle to demonstrate the maximum convertibility of heat into work. any fluid can be used to operate the Carnot cycle which is performed in an engine cylinder the head of which is suppose alternatively to be perfect conductor or a perfect insulator of the heat.
Following are assumptions which are made by Carnot engine during its working:
(i) The piston moving in a cylinder does not develop any friction during motion.
(ii) The walls of the piston and cylinder are considered to be perfect insulators of heat.
(iii) The transfer of the heat does not affect the temperature of source or sink.
(iv) Working fluid is taken as an ideal gas.
(v) Compression and expansion are reversible.
The system consists of one mole of an ideal gas which is subjected to a series of four successive operations, commonly termed as four strokes, which are discussed below and consider the figure below
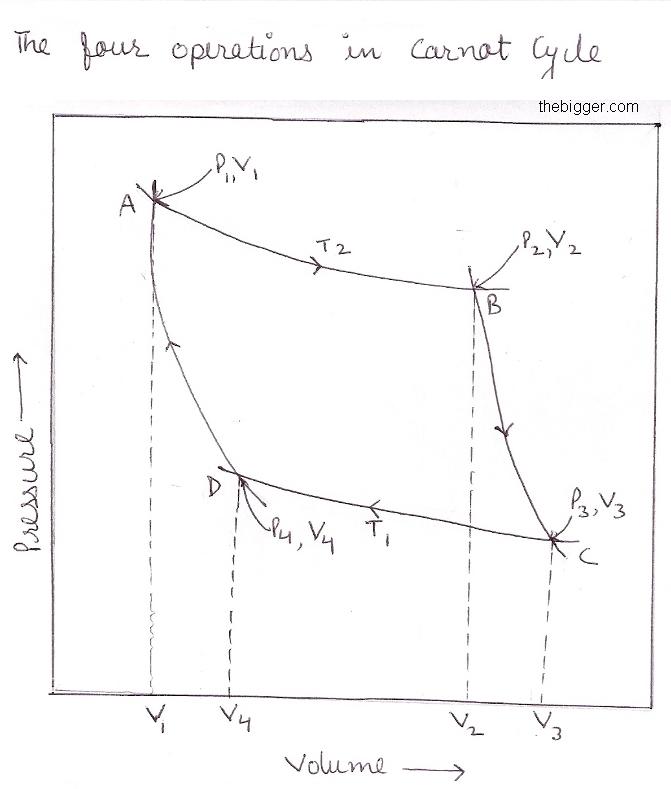
Stage 1: Isothermal Expansion (Stroke 1, process A-B):
The gas is allowed to expand reversibly and isothermally at the temperature T2 so that the volume increases from V1 to V2 represented by the points A and B respectively.
As in isothermal expansion of the ideal gas internal energy change is equal to zero hence, the heat absorbed is equal to the work done by the system on the surroundings. Suppose q2 be the heat absorbed by the system from the surroundings at temperature T2 and w1 be the work done by the surroundings. Then,
q2 = – w1 = R T2 ln (V2 / V1) ………… (1)
Stage 2: Adiabatic Expansion (Stroke 2, process B-C):
Here the cylinder becomes a perfect insulator so that no heat flow takes place. The gas is the allowed to expand reversibly and adiabatically from the volume V2 to V3 i.e. form point B to C.
As work is being done by the system adiabatically, heat is not being absorbed. The temperature of the system decreases from T2 to T1. As cylinder is a perfect insulator so heat q is equal to zero. Hence from the first law of equation, ∆U = w. as the process is expanded, work is done by the system on the surroundings. Hence work done will be negative i.e. ∆U = – w.
Now, Cv = (∂U / ∂T) v
∆U = Cv ∆T = Cv (T1 – T2) = – w
As change in temperature ∆T = final temperature – initial temperature
= T2 – T1
Therefore, – w = – Cv (T2 – T1)
If work done is considered as w2, then
– w2 = – Cv (T2 – T1) …………………….. (2)
Stage 3: Isothermal Compression (Stroke 3, process C-D):
After this, the gas is allowed to compress reversibly and isothermally at the lower temperature T1 so that the volume decreases from V3 to V4 represented by the points C and point D respectively. The work is done on the system. Hence heat is evolved to the surroundings. As in isothermal compression of the ideal gas internal energy change is equal to zero i.e. ∆U = 0. If q1 is the heat evolved in the surroundings at temperature T1 and w3 is the work done on the system, then,
-q1 = w3 = R T1 ln (V4 / V3) ………… (3)
Stage 4: Adiabatic Compression (Stroke 4, process D-A):
Here the cylinder becomes a perfect insulator so that no heat flow takes place. The gas is the allowed to compress reversibly and adiabatically from the volume V3 to original volume V1 i.e. form point D to A.
As work is being done on the system adiabatically, heat is not being absorbed. As cylinder is a perfect insulator so heat q is equal to zero. Hence from the first law of equation, ∆U = w. as the process is expanded, work is done on the system by the surroundings. Hence work done will be positive i.e. ∆U = w
Hence, ∆U = w = Cv ∆T = Cv (T2 – T1)
If work done is considered as w4, then
w4 = Cv (T2 – T1)
Where T2 – T1 is the increase in temperature produced by the adiabatic compression.
The net heat absorbed (q) by the ideal gas during the whole cycle is given as:
q = q2 + (-q1) = R T2 ln (V2 / V1) +
R T1 ln (V4 / V3)
= R T2 ln (V2 / V1) –
R T1 ln (V3 / V4)
Or q = q2 – q1 = R (T2 – T1) ln (V2 / V1)


