Show that for an ideal gas, the work differential dw is not an exact differential.

We know that work differential dw is calculated as:
dw= PdV ……………. (1)

since volume V is a state function i.e. it is independent of the path [V=f (T,P)] hence dV is an exact differential.Therefore

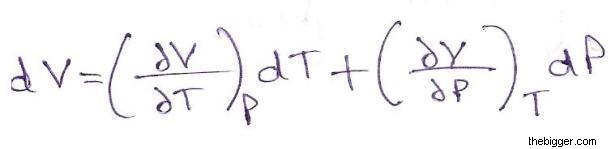……. (2)

For an ideal gas, we know that PV = RT which means:

V= RT/P

Hence,
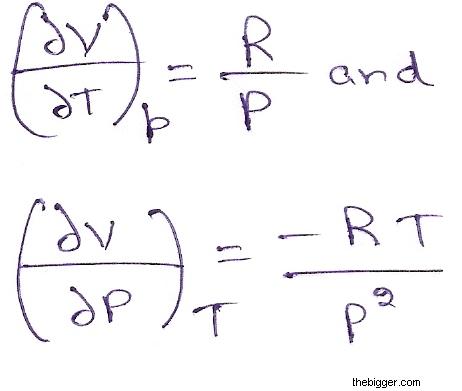……… (3)

Substituting the Equations (1) and (2) in equation (1), we get:

dw = PdV = RdT – (RT/P) dP = RdT – VdP …………………. (4)

Applying the Euler reciprocal relation to equation (4), we get

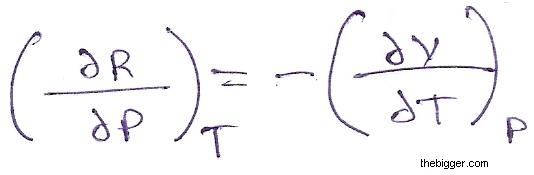
Since R is the gas constant, hence (∂R/∂P) _T = 0 ……… (5)

Accordingly, from equation (5), (∂V/∂T) _P = 0

But it brings contradiction as there is always a change in volume with temperature at constant pressure. This leads to the conclusion that dw is not an exact differential.